0w0
빅데이터 분석 내용 정리 본문
PART 3 빅데이터 모델링
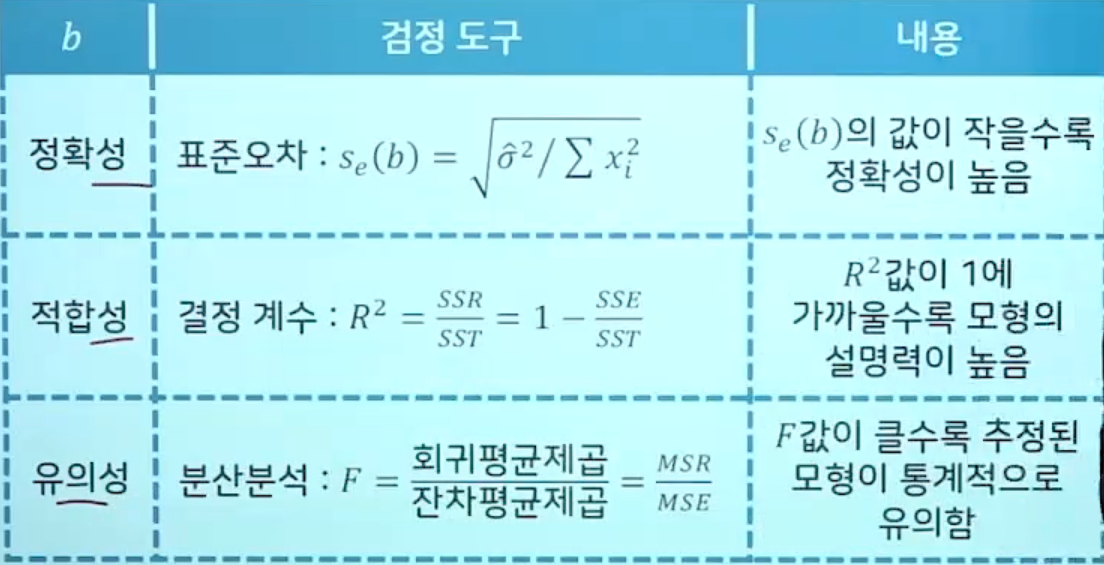
*통계분석 기법 : AIC와 BIC를 이용해 평가 및 선택
1. 전진선택법
- 반응 변수와 상관관계가 가장 큰 설명 변수부터 단계적으로 선택하는 방법임
- 이해가 쉽고 변수의 개수가 많은 경우에도 사용가능하지만 안정성이 떨어짐
2. 후진제거법
- 완전모형에서 설명력이 작은 변수부터 하나씩 제거해 나가는 방법임
- 독립변수를 모두 추가한 상태에서 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 제거할 변수들이 없을 때까지 진행함
- 전체 변수를 모두 이용한다는 장점이 있지만 변수의 개수가 많을 경우 사용이 힘들다는 단점이 있음
3. 단계별 선택법
- 전진선택법에 의해 각 단계별 새로 추가된 변수에 기인해 기존 변수의 중요도가 약화되면 해당 변수를 제거하는 등 단계별로 추가 또는 제거된 변수들의 중요도를 다시 검사하여 변수를 제거하는 방법임
- 제거할 변수가 없을 때까지 진행함
*변수선택 및 차원축소 모형
데이터 정제 -> 변수 간의 상관관계 파악 -> 전체모형 결정 -> 변수선택 -> 최적모형 결정
*가설검정 절차
가설설정 -> 의사결정규칙 설정 -> 데이터수집 및 가설검정을 위한 통계량 계산 -> 의사결정 -> 사후조치
*통계적 가설 : 모집단의 '모수'에 대해 설정하는 것을 말함
*가설검정 : 모수에 대한 서로 경쟁적 상호 배타적이며 포괄적인 두개의 가설을 설정하고, 이 중에서 어느 가설을 택할지 결정하는 것을 말함
*추정방법
1. 최우도 추정법, 최소제곱 추정법
- 전통적 추정방법
- 표본의 데이터로부터 표본평균을 구하여 추정치로 사용
2. 베이지안 추정
- 초기 추정치를 설정한 후 더 그럴듯한 추정치로 바꾸어 나가면서 최종의 추정치로 사용함
*전통적 추정과 베이지안 추정 방법의 차이점
1. 데이터에 대한 의존도의 차이
- 전통적 추론은 주어진 모집단 데이터가 없어 먼저 표본을 만든 후 표본 데이터 100% 의존하여 추론
- 베이지안 추론은 데이터에 대한 의존도를 사람의 판단에 의해 신축적으로 조정 가능함
2. 모수와 변수를 보는 시각의 차이
- 전통적 추론 : 모수는 참값을 알 수 없는 고정된 상수, 데이터는 확률분포를 따라 움직이는 변수라고 가정함
- 베이지안 추론 : 모수도 여러개의 값을 가질 수 있는 변수이며 확률분포라고 가정함
3. 추정의 실질적 목적의 차이
- 전통적 추론 : 모집단 전체에 대한 추측을 주목적으로 하여 추정에 초점을 맞춤
- 베이지안 추정 : 새로운 관측치에 대한 예측에 더 큰 관심을 두고, 의사결정이나 전략적 판단에 필요한 정보의 수집에 초점을 맞춤
*추정의 과정
1단계 : 베이즈 정리의 도입
2단계 : 추정문제의 설계
3단계 : 사전분포의 설정
4단계 : 초기 추정치 설정
5단계 : 확률분포 수정
6단계 : 사후분포 도출
7단계 : 최종 추정치 도출의 과정
*분석 모형 구축절차
1. 하향식 분석 프로세스
- 분석 모형 기획의 현황 분석을 통해서 또는 인식된 문제점, 전략으로부터 기회나 문제를 탐색하면서 시작됨
2. 상향식 분석 프로세스
- 명확한 문제 해결절차를 수용하지 않음
- 보유하고 있는 데이터웨어하우스나 데이터마트 등에 존재하는 변환 정체 과정을 거친 데이터를 기반으로, 기본적인 기술적 통계분석, 군집분석, 시각화 기법, 상관분석, 인과 분석 등을 통하여 데이터에 내재되어 있는 유의미한 패턴과 관계 집합을 도출함
- 문제나 기회를 발견할 수 있음
3. 프로토타이핑 프로세스
- 사용자의 개괄적인 요구 사항을 반영한 초기 프로토타입 모델의 개발로부터 시작됨
- 차후에 수정한다는 전제하에 사용자의 기본적인 요구만을 반영하여 최대한 짧은 시간 내에 만들어낸 분석 모형 시스템임
- 사용자 요구 사항의 완전성에 직접적인 영향을 받으며 아래와 같은 항목 등에 의해 간접적 영향을 받을 수 있음
*분석도구
1. SPSS
- 데이터분석에서 가장 많이 사용되는 분석 툴
- 1970년대 시카고대학 개발
- 마우스 클릭을 통한 UI, 쉬운 조작과 분석
- 라이선스가 비쌈, 구버전 파이썬과 연동
2. SAS
- 1970년대 미국 노스캐롤라이나대학 개발
- 분석 및 모델링 등 선택이 다양하고 프로그램의 융통성이 큰 편
- 복잡한 UI와 코드, 라이선스가 비쌈
3. MINITAB
- 1972년 펜실베이니아 주립대학 개발
- 개인용 PC에서 쉬운 조작, 공장 및 생산라인에서 분석용으로 사용됨
*오픈소스 툴
1. R
- 데이터 분석에 특화되어 있음
- 통계학자들이 개발한 툴로서 주로 데이터 분석을 수행함
- CRAN 이라는 오픈소스에는 분석부터 머신러닝, 딥러닝까지 만오천개가 넘는 패키지가 있음
- 다양한 라이브러리를 이용한 세부적인 분석 가능, 데이터 시각화 용이
2. python
- 프로그래밍 언어로 범용
- 기계학습 및 인공지능을 위한 API를 빠르게 제공받을 수 있음
*데이터
- 학습데이터 / 테스트데이터
- 일반적으로 학습 데이터와 테스트 데이터의 크기는 7:3 혹은 8:2로 분리함
*데이터의 차원축소
- 차원축소는 불필요한 변수를 줄여서 분석 시간을 절약
- 예측 성능 향상에 기여하며, 다차원 데이터의 차원을 줄여 패턴을 시각적으로 제공
*차원축소분석 방법
1. 주성분분석(PCA)
- 가장 대표적인 차원축소분석
- 많은 변수에서 주성분이라는 새로운 변수를 생성, 기존 변수보다 차원을 축소해 분석을 수행
- 고차원의 원본 데이터를 저차원의 부분 공간으로 투영하여 데이터를 축소하는 기법임
- 원본 데이터의 변동성을 가장 중요한 정보로 생각함
- 원본 데이터의 변동성을 기반으로 첫번째 벡터 축을 생성, 두번재 벡터 축을 첫 번째와 직각이 되는 벡터 축으로 설정함
- 생성된 벡터에 원본 데이터를 대입하면 벡터 축의 개수만틈 원본 데이터의 차원이 축소됨

2. 선형판별분석(LDA)
3. 다차원척도분석(MDS)
*회귀분석
- 변수 간의 원인과 결과 간의 인과 관계를 설명하는 분석 방법
- 독립변수(연속형)와 종속변수(연속형) 간의 관계를 함수관계로 나타내고 독립변수가 종속변수에 미치는 영향의 정도를 분석함
*회귀분석의 추정 방법
1. 최소자승법 (가장많이 쓰임)
2. 최우도법
3. 베이지안법
4. 적률법
*단순 회귀분석 : 독립변수의 수가 1개 일 경우 이용 (입력변수가 단수인 경우)
*다중 회귀분석 : 독립변수의 수가 2개 이상 일 경우 이용 (입력변수가 다수인 경우)
*로지스틱 회귀분석 : 종속변수가 이향형 또는 순서형으로 나타나는 경우 이용
*통계학에서 통계 결과치에 대한 검정 방법
1. T-검정 : 비율척도 자료에 적용, 2집단 간의 비교에 적용
2. F-검정 : 비율척도 자료에 적용, 3집단 이상간의 비교에 적용
3. X^2-검정 : 명목척도 자료에 적용
*희귀분석은 크게 두 분류
- 일반적인 회귀 모형 : 추정할 종속변수의 유형이 연속형일 경우
- 로지스틱 회귀 모형 : 추정할 종속변수의 유형이 이항형 또는 순서형의 범주형 자료 형태일 경우
*로지스틱 회귀
- 선형 회귀분석과는 다르게 종속변수가 범주형 데이터를 대상으로 함
- 입력데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류 기법으로도 볼수 있음
- 로지스틱 회귀는 종속변수가 이항형 문제(유효한 범주의 개수가 두개인 경우) 또는 순서형의 범주형 자료 형태를 지칭할 때 사용됨
- 예) 기획한 상품의 성공 OR 실패(종속변수가 이항형 문제)를 분석할 떄 사용
- 로지스틱 회귀는 이항형 또는 다항형이 될 수 있음
- 이항형 로지스틱 회귀 : 종속변수의 결과가 (성공,실패) 2개의 카테고리가 존재하는 것을 의미, 2개의 카테고리는 0과 1로 나타내고 각각의 카테고리로 분류될 확률의 합은 1이 됨
- 다항형 로지스틱 회귀 : 종속형 변수가 (맑은,흐림,비)와 같이 2개 이상의 카테고리로 분류되는 것을 의미함
*연결함수의 대표적인 형태

*로지스틱 모형 : 독립변수가 어느 숫자이든 상관없이 종속변수 또는 결괏값이 항상 [0,1] 사이에 있도록함
- 이는 오즈(odds)를 로짓(logit) 변환함으로써 얻을 수 있음
*오즈(odds) : 성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타냄

*로짓(logit) 변환 : 오즈에 로그를 취한 함수로서 입력 값의 범위가 [0,1]일 때 출력값의 범위를 (-∞,∞) 로 조정함

*로지스틱 함수
1. 다항 로지스틱 회귀(분화 로지스틱 회귀) : 두 개 이상의 범주를 가지는 문제가 대상인 경우
2. 서수 로지스틱 회귀 : 복수의 범주이면서 순서가 존재하는 경우
*다중선형회귀모형
- 목표변수 y의 관찰 값이 이항형이지만 예측 값의 유형이 이항형이 아닐 경우 문제가 생길 수 있음
- y의 예측값 범위가 [0,10]이였지만 예측값을 벗어나게 되는 문제가 생길 수 있음
- 목표 변수 y에 대한 확률분포가 선형회귀에 가정되는 확률분포와 맞지 않는다는 것임
- 위에 문제를 해결하기 위해 로짓변환(logit transformation)을 고려하여 분석함 -> 로지스틱 회귀모형
*로지스틱 회귀모형
- 로지스틱 회귀 분석은 의료, 통신, 데이터마이닝과 같은 다양한 분야에서 분류 및 예측을 위한 모델로서 폭넓게 사용되고 있음
- y를 [0,1] 로 변환
*의사결정나무 기법
- 의사결정나무는 데이터마이닝의 주요 기법 중 하나로서 경영, 경제에 관련된 다양한 분야의 분류 및 예측에 주로 사용됨
- 목표변수에 대한 의사결정 규칙(rule)들을 나무구조로 그래프화하여 분류하여 예측을 수행하는 방법으로, 각종 데이터로부터 규칙을 도출하는 데 유용함

*의사결정나무 장점
- 다른 통계기반 기법에 비해 분석결과의 해석이 쉬움
- 어떠한 변수들이 분류에 중요한 영향을 미치는지 설명이 가능함
- 변수들 간의 상호작용에 대한 해석이 용이함
- 모형 구축 시간이 길지 않음
*의사결정나무 분석의 단계
- 의사결정나무의 형성 -> 가지치기 -> 타당성 평가 -> 해석 및 예측
- 의사결정나무의 형성 : 분석의 목적과 자료구조에 따라서 적절한 분리기준과 정지규칙을 지정하여 의사결정나무를 얻음
- 가지치기 : 분류오류를 크게 할 위험이 높거나 부적절한 추론규칙을 가지고 있는 가지를 제거함
- 타당성 평가 : 이익도표나 위험도표 또는 검즘용 자료에 의한 교차타당성 등을 이용하여 의사결정나무를 평가함
- 해석 및 예측 : 의사결정나무를 해석하고 예측모형을 설정, 이진트리구조, 이진트리구조 뿐만 아니라 혼합된 형태의 모형도 있음
*의사결정나무 알고리즘 : 분리기준과 정지규칙 그리고 가지치기 등에서 서로 다른 차이점을 갖음
- CART : 지니지수(gini index) 또는 분산의 감소량을 분리기준으로 활용하고 이진분리를 수행함
- C4.5 알고리즘 : 엔트로피지수를 분리 기준으로 활용함
- CHAID : 카이제곱-검정 또는 F-검정을 분리기준으로 활용하고 다시 분리 수행이 가능함
*의사결정나무 장점
- 주요 변수의 선정이 용이 : 중요한 변수만 선별하여 의사결정나무를 구성함
- 교호효과의 해석 : 두개 이상의 변수가 결합하여 목표변수에 어떻게 영향을 주는지 쉽게 알 수 있음
- 비모수적 모형 : 선형성, 정규성, 등분산성 등의 가정이 필요없음
- 해석의 용이성 : 모형 및 자료, 목표 변수 설명이 쉬움
- 지식의 추출 : 의사결정나무를 룰로 자동변화가 가능하며, 다양한 방식으로 룰을 활용
*의사결정나무 단점
- 비연속성 : 연속형 변수를 비연속적인 값으로 취급하기 때문에 분리의 경계점 근방에서 예측 오류가 클 가능성이 있음
- 선형성 결여 : 선형 예측에 좋은 결과를 얻을 수 없다는 한계점이 있음
- 비안정성 : 분석용 자료에만 의존하기 때문에 새로운 자료의 예측에서는 불안정할 가능성이 높음
- 몇몇 의사결정나무 알고리즘이 이진분리를 이용하기 때문에 분리 가지의 수가 너무 많음
- 나무형성 시 컴퓨팅 비용이 많이 듦
*의사결정나무의 분리원칙
- 부모마디의 순수도에 비해서 자식마디들의 순수도가 증가하도록 자식마디를 형성해 나감
- 목표변수의 분포를 구별해 주는 정도는 순수도 또는 불순도에 의해 측정되는데, '목표변수의 특정범주에 개체들이 포함되어 있는 정도'를 순수도라고함
- 목표변수가 이산형이냐 연속형이냐에 따라 각각 분리기준을 달리함
*의사결정나무_이산형 목표변수에 사용되는 분리기준
- 이산형 목표변수의 경우 목표변수의 각 범주에 속하는 빈도(frequency)에 근거하여 분리가 일어남
- 분리기준
1. 카이제곱통계량의 유의확률
2. 지니지수
3. 엔트로피지수
*카이제곱통계량의 유의확률
- 범주형 자료에서순도에 대한 차이 유무에 대한 검정결과로 얻어지는 유의확률로서 유의확률이 작은 입력변수와 그때의 분리기준에 의해서 자식마디가 형성됨
- 카이제곱통계량은 (기대도수-관측도수)^2/기대도수의 합
*지니지수(Gini index)
- 불순도를 측정하는 하나의 지니로서 지니지수를 가장 감소시켜주는 입력변수와 그때의 최적 분리기준에 의해 자식마디가 형성됨
*엔트로피지수(Entropy index)
- 다항분포에서 우도비 검정통계량을 사용하는 것으로 이 지수가 가장 작은 예측변수와 그때의 최적분리에 의해 자식마디가 형성됨
*정지규칙(Stopping rule)
- 의사결정나무에서 정지규칙은 더 이상 분리가 일어나지 않고 현재의 마디가 잎이 되도록 하는 규칙
- 정지규칙의 규칙
1. 모든 자료가 한 그룹에 속할 때
2. 마디에 속하는 자료가 일정 수 이하일 때
3. 불순도의 감소량이 아주 작을 때
4. 뿌리마디로부터의 깊이가 일정 수 이상일 때
*가지치기 규칙(Pruning)
- 성장이 끝난 나무의 가지를 적당히 제거하여 적당한 크기를 갖는 나무모형을 최종적인 예측모형으로 선택하는 것이 예측력의 향상에 도움이 됨
- 지나치게 많은 마디를 가지는 의사결정나무는 새로운 자료에 적용할 때 예측오차(prediction error)가 매우 클 가능성이 있음
- 형성된 의사결정나무에서 적절하지 않은 마디를 제거하여 적당한 크기를 갖는 부분 의사결정나무를 최종적인 예측모형으로 선택하는 것이 바람직함
*CHAID
- 목표변수 : 명목형, 순서형, 연속형
- 예측변수 : 명목형, 순서형, 연속형(사전그룹화)
- 분리기준 : 카이제곱-검정, F-검정
- 분리개수 : 다지분리
- 가지치기 : 알고리즘에 포함되어 있지 않음
- 결손값의 대체규칙 : 알고리즘에 포함되어 있지 않음
- 비용함수 : 변수선택에 직접적으로 사용되지 않음
- 초기 자동교호감지 시스템 AID로 부터 유래됨
- 변수 간의 통게적 관계를 알아내기 위하여 사용되었으며, 변수들 간의 상관관계를 이용하여 의사결정나무를 만들어야 하므로 의사결정나무에서 분류를 위한 도구로 사용됨
- 과다적합하고 나서 가지치기를 하지 않고 과다적합이 일어나기 전에 나무를 키워나가는 것을 중지하고 범주형 변수에만 국한되어 사용됨
- 연속형 변수는 범위로 나눠어져 상 중 하 등의 범주형 계급으로 대체되어야함
- 자식마디들은 목표변수의 특정한 값에 대한 확률이 마디마다 다르도록 선택됨
- 일부에서는 여전히 가지치기는 실제 관측치에 대해 나무의 역할을 반영하지 않는 단순화된 나무를 만든다 하여 CHAID 로 접근하는 것을 선호함
*CART
- 목표변수 : 명목형, 순서형, 연속형
- 예측변수 : 명목형, 순서형, 연속형
- 분리기준 : 지니계수, 분산의감소
- 분리개수 : 이지분리(Binary)
- 가지치기 : 알고리즘에 포함되어 있음
- 결손값의 대체규칙 : 알고리즘에 포함되어 있음
- 비용함수 : 변수선택에 사용됨
- 의사결정나무를 만드는데 가장 많이 사용되는 방법 중 하나
- 지니지수(이산형 목표변수인 경우 적용), 분산의 감소량(연속형 목표변수인 경우 적용)을 이용하여 이진분리
*QUEST
- 목표변수 : 명목형
- 예측변수 : 명목형, 순서형, 연속형
- 분리기준 : 카이제곱-검정, F-검정
- 분리개수 : 이지분리(Binary)
- 가지치기 : 알고리즘에 포함되어 있음
- 결손값의 대체규칙 : 알고리즘에 포함되어 있음
- 비용함수 : 변수선택에 직접적으로 사용되지는 않으나 비용함수에 의해서 사전확률을 조정함
- 목표변수의 범주가 3개 이상인 경우에는 2평균 군집분석을 수행하여 두개의 그룹을 만든 후 분석을 수행
- 각 예측변수의 최적분리를 찾기 위하여 2차 판별분석을 수행하고, 목표변수를 가장 잘 분류하는 예측변수의 최적분리를 이용하여 자식마디를 형성함
- 변수선택편의(Bias)나 계산시간을 줄이고자 하는 방법
- 관측치의 수가 많거나 복잡한 자료에 대해서는 효율적
*의사결정나무의 활용
- 대형 데이터 집합을 탐색하여 유용한 변수를 골라내기
- 주요 산업 공정 등에서 중요한 변수들의 미래 상태를 예측하기
- 추천 시스템에 대한 방향성 있는 고객의 군집을 형성하기
*인공신경망
- 인공신경망 모형은 예측 오차를 줄이고 예측 정확성을 증진시키기 위해서 반복적으로 가중치를 수정함
- 반복적인 단계를 훈련이라고함
- 노드와 노드의 연결 및 그 연결에 부여된 가중치로 구성되어 있는 체계적 모형인 암흑상자(블랙박스)
- 자기조직화를 찾기 떄문에 해 또는 결과를 도출하는 과정에서는 많은 유연성을 갖고 있음
- 각 입력노드로부터 전달되는 신호들을 모아 선형결합함
- X1,....,Xp를 설명변수(입력노드)라고 할 때 은닉노드 L 공식
- 은닉노드가 다수인 경우 가중치 W1...+Wp는 노드에 따라 다르게 됨

- 은닉노드 L이 클수록 뉴런이 많이 활성화되고 작을 수록 조금 활성화됨
- 뉴런의 활성화 정도를 S라고 하면, S가 제한된 범위의 값을 취하도록, L로 부터 S로의 변환 S=g(L)에 시그모이드형 곡선이 개입됨

*은닉노드(뉴런)
- 입력노트로부터 전달되는 신호들을 모아 선형결합함
- 은닉노드 L이 클수록 뉴런이 많이 활성화되고 작을 수록 조금 활성화됨
*역전파 알고리즘(Back-propagation Algorithm)
- 효율적인 계산을 위한 반복 학습
- 학습률과 모멘트 두가지 요소가 있음
- 임의의 위치에서 시작하되 큰학습률 η를 적용하여 적극적으로 학습시키지만 점차 작은 학습률을 채택함
- 결국 최대점이라고 생각되는 곳에 도달함
- 다시 다른 임의의 위치에서 시작하되 동일한 과정을 반복함
- 위의 과정을 무수히 반복하여 가장 높은 최대점을 취함으로써, 최종 도달한 곳이 국소(Local) 최대점이 아닌 대역(Global) 최대점, 또는 그것에 가깝게 되도록함
- 흔히 모멘트 α 값은 고정됨
- 이런 식으로 가능도(Likelihood)가 최대가 되는 가중치 파라미터들을 찾아내기 때문에 훈련자료에서만 통하는 과다한 최대화가 추구되기 십상임, 과적합(Over fitting)
- 과적합(over fitting)을 막기 위하여 실제로 훈련자료의 일부만 최적 파라미터를 찾는 데 쓰고 남은 일부는 가능도 값을 산출하는데 씀
*학습률(η)
- η>0
- 경사가 가장 높아지는 방향으로 올라가도록 함
- 적극성을 뜻함
*모멘트(α)
- α>0
- 이제까지 이동하던 방향으로 움직이도록 함
- 안정성을 위함
*인공신경망
- 자료의 관련성을 나타내 줄 수 있는 기법으로, 뇌의 신경시스템을 응용하여 예측을 최대화하기 위한 조직화를 찾기 위해 반복적으로 학습하는 원리임
- 복잡하고 비선형적이며 관계성을 갖는 다변량을 분석을 할 수 있음
*인공신경망의 장점
- 회귀분석과 같은 선형 기법과 비교하여 비선형 기법으로서의 예측력이 뛰어남
- 자료에 대한 통계적 분석 없이 결정을 수행할 수 있음
- 통계적 기본가정이 적고 유연하며 다양하게 활용 가능
- 데이터 사이즈가 작은 경우나 불완전 데이터, 노이즈 데이터가 많은 경우 인공신경망 모델의 성능이 일반적으로 다른 기법과 비교해서 우수하다고 평가
*인공신경망의 단점
- 모델이 제시하는 결과에 대하여 왜 그런결과가 나오는지에 대한 원인을 명쾌하게 설명할 수 없음(블랙박스)
- 모델의 학습에 시간이 과도하게 듦
- 전체적인 관점에서의 최적해가 아닌 지역 내 최적해가 선택될 수 있음
- 과적합화(overfitting)가 될 수 있음
*인공신경망 구축 시 고려사항
1. 입력변수
- 입력자료를 선택하는 문제
- 연속형 입력변수의 변환 또는 범주화
- 새로운 변수의 생성
- 범주형 입력변수의 가변수화
2. 초기치와 다중 최솟값 문제
- 역전파 알고리즘은 초깃값에 따라 그 결과가 많이 달라지므로 초기치의 선택은 현실적으로 매우 중요한 문제
- 만약 가중치가 0이면 시그모이드 함수는 대략 선형이되고 따라서 신경망 모형은 근사적으로 선형모형이됨
- 보통 초기치는 0근처에서 랜덤하게 선택되므로 초기의 모형은 선형모형에 가깝고 가중치 값이 증가할수록 비선형모형이됨
- 신경망에서 일반적으로 비용함수 R(θ)은 비볼록함수 이고 여러 개의 국소 최솟값(local minima)를 가짐
- 랜덤하게 선택된 여러 개의 초기치에 대하여 신경망을 적합한 후 얻은 해들을 비교하여 가장 오차가 작은 것을 선택하여 최종 예측치를 얻거나 예측값의 평균(또는 최빈값)을 구하여 최종 예측치로 선정하는 방법을 고려해 볼 수 있음
- 훈련자료에 대하여 신경망을 기저 학습법으로 사용하는 배깅(Bagging)을 적용하는 것이 있음
3. 학습모드와 학습률(역전파 알고리즘 실행 시 많이 사용되는 방법)
- 온라인 학습모드 : 각 관측값을 순차적으로 하나씩 신경망에 투입하여 가중치 추정값을 매번 조정함
- 확률적 학습모드 : 온라인 학습모드의 변형으로 신경망에 투입되는 관측값의 순서가 랜덤임
- 배치 학습모드 : 훈련자료 전체를 동시에 신경망에 투입하여 역전파 알고리즘으로 값을 구함
4. 은닉층과 은닉노드의 수
- 은닉노드의 수는 기본적으로 자료의 성격이나 상황에 따라 결정해야함
- 은닉노드의 수는 교차확인오차를 사용하여 결정하는 것보다는 적절히 큰 값으로 놓고 가중치 감소라는 모수에 대한 벌점화를 적용하는 것이 좋음
5. 과대적합 문제
- 신경망에서는 많은 가중치를 추정해야 하므로 과대적합 문제가 빈번히 발생함
- 과대적합을 피하기 위한 방법은 아래와 같은 두가지 방법이 있음
- 알고리즘의 조기 종료
- 가중치 감소 기법
*배깅(Bagging)
- bootstrap aggregating의 준말
- 주어진 자료에 대하여 여러 개의 부트스트랩 자료를 생성하고 각 부트스트랩 자료에 예측모형을 만든 후 결합하여 최종 예측모형을 만드는 방법
*부트스트랩 자료
- 주어진 자료로부터 동일한 크기의 표본을 랜덤 복원추출로 뽑은 자료
*훈련용 데이터
- 모델을 만드는 데 사용되는 데이터를 말함
*테스트 데이터
- 모델 검증을 위한 데이터
- 모델의 정확도, 예측력을 테스트하기 위해 사용됨
*서포트벡터 머신(SVM:Support Vector Machines)
- SVM은 데이터로부터 분류와 규칙을 학습하기 위한 훈련 알고리즘으로서 통계적 학습 이론을 기반으로 하고 있음
- SVM의 기본 원리는 훈련데이터들을 서로 다른 두개의 클래스로 분류할 때 기준이 되는 분리경계면을 학습 알고리즘을 이용하여 찾는 것임
- 일반적으로 분류 또는 회귀분석에 사용가능한 초평면(hyperplane) 또는 초평면들의 집합으로 구성되어 있음
- 좋은 분류를 위해서는 어떤 분류된 점에 대해서 가장 가까운 학습 데이터와 가장 먼 거리를 가지는 초평면을 찾아야함
*연관관계분석
- 상품 혹은 서비스 간의 관계를 살펴보고 이로부터 유용한 규칙을 찾아내고자 할 때 이용될 수 있는 기법임
- 동시 구매될 가능성이 큰 상품들을 찾아내는 기법으로 시장바구니분석과 관련된 문제에 많이 적용되어 왔음
- 측정의 기본은 '얼마나 자주 구매되었는가' 하는 빈도를 기본으로, 연관정도를 정량화하기 위해서 지지도, 신뢰도, 향상도를 계산하여 기준으로 함
- 데이터마이닝을 이용해서 연관성 규칙을 발견하는 것은 대량의 데이터로부터 품목 간에 어떠한 종속관계가 존재하는지를 찾아내는 작업으로, 이를 통해 요소 간의 연관성 패턴을 분석할 수 있음
- 동시에 구매될 확률이 높은 상품 및 상품 간의 관계를 찾아낼 수 있어 장바구니 분석에 많은 사용됨
- 연관성 규칙은 데이터들의 빈도수나 동시발생 확률을 이용하여 한 항목들의 그룹과 다른 항목들의 그룹 사이에 강한 연관성이 있음을 밝히는 기술임
- 대량의 데이터로부터 연과성을 도출하기 위해서 필요한 기준 : 지지도, 신뢰도, 향상도
*지지도(support) : 전체 거래 중에서 어떠한 항목과 다른 항목 사이에 동시에 포함되는 거래의 빈도가 어느 정도인가를 나타냄
*신뢰도(confidence) : 조건부확률과 동일한 방식으로 정의됨(X->Y , X상품을 구매했을 때 Y상품을 같이 구매할 확률)
*향상도(lift) : X상품을 구매했을 때 그 거래가 다른 Y상품을 포함하는 경우 Y상품이 X와 상관없이 단독으로 구매된 경우와 비율을 의미함
*연관성 규칙
- 두 항목 간 그룹 사이에 강한 연관이 존재하는지에 대한 기술을 말함
- A라는 사건이 일어나면 B라는 다른 사건이 일어난다
- 연관성 규칙은 비목적성 기법으로, 목적 변수 없이 규칙 관계를 설명할 수 있고 구체적인 행위를 언급하여 규칙을 도출하기 때문에 이해하기 쉽고 명쾌함
- 실질적인 정보를 도출할 수 있는 장점을 가지고 있어 마케팅 문제뿐만 아니라 광범위한 의사결정을 하는 데 널리 사용됨
*연관관계분석의 장점
1. 결과가 분명함 : 조건->결과
2. 간접적 데이터마이닝에 유리함
3. 한 개의 변수가 여러 개의 값을 갖는 데이터에 유리함
4. 계산이 용이함
*연관관계분석의 단점
1. 품목이 많아지면 계산량이 기하급수적으로 필요
2. 자료속성에 따라 제한된 지원을 함
3. 적절한 품목을 결정하기가 어려움
4. 거래가 드문 품목을 무시함
*군집분석(Cluster Analytics)
- 군집분석은 전체 데이터를 군집을 통해 구분하는 것
- 다양한 특징을 가진 관찰 대상으로부터 동일 집단으로 분류하는 데 사용함
- 유사한 특성을 가진 개체를 합쳐가면서 최종적으로 유사 특성의 군집을 찾아내는 분류방법
- 구분하려고 하는 각 군집에 대한 아무런 사전지식이 없는 상태에서 분류하는 것
- 무감독학습(Unsupervised Learning)
- 사전지식 없이 유사도에 근거하여 군집을 구분
- 개체 집합을 군집(cluster), 군집화하는 과정을 클러스터링(clustering)
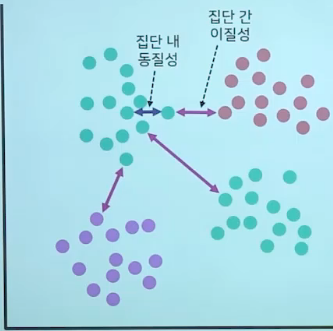
*군집분석_거리측정함수
1. 유클리드 거리
2. 마할라노비스 거리
3. 헤밍 거리
*군집분석 분류
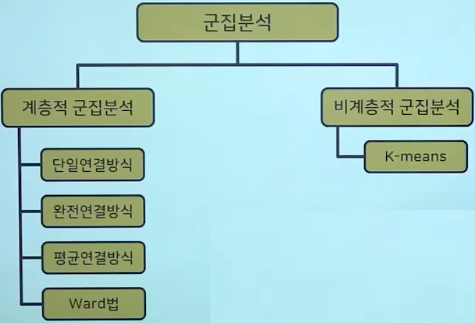
*계층적 군집분석
- 개별대상 간의 거리에 의하여 가장 가까이에 있는 대상들로부터 시작하여 결합해 감으로써 나무모양의 계층구조를 형성해 가는 방법임
- 덴드로그램을 그려줌으로써 군집이 형성되는 과정을 정확히 파악할 수 있으나 데이터의 크기가 크면 분석하기가 어렵다는 단점이 있음
- 한 개체가 일단 특정 군집에 소속되면 다른 군집으로 이동될 수 없으며, 예욋값(outlier)이 제거되지 않고 반드시 어느 군집에 속하게 된다는 한계점을 가짐
1. 단일연결방식
- simple linkage, nearest neighbor method
- 군집 간의 거리를 한 군집에 속한 개체와 다른 군집에 속한 개체 간의 거리가 가장 가까운 개체 간의 거리로 계산하여 연결하는 방식
2. 완전연결방식
- complete linkage, furthest neighbor method
- 군집 간의 거리를 두 군집 간의 거리가 가장 먼 개체 간의 거리로 계산하여 연결하는 방식
3. 집단 간 평균 연결 방식
- average linkage between groups method
- 군집 간 각 개체 간의 거리를 평균하여 이 평균거리가 가장 가까운 집단을 연결하는 방식
4. 집단 내 평균 연결 방식
- average linkage within groups method
- 집단 간 평균 방식의 변형으로 다른 군집에 있는 개체간의 거리뿐만 아니라 같은 집단에 속한 개체간의 거리도 포함하여 평균을 구하는 방식
5. Ward법
- Ward의 오차제곱합
- 단순한 거리 기준이 아닌, 구성 가능한 군집들 모두에 대해서 그 군집을 구성하는 대상들의 측정치의 분산을 기준으로 사용하는 방법
*비계층적 군집분석
- 군집분석에서 개체의 수가 많은 경우에는 개체들 간의 유사성을 구하는 것이 번거롭고 어려운일임
- 비계층적 군집분석은 계층적 군집분석과 달리 군집의 수가 한개씩 감소하는 것이 아니라 사전에 정해진 군집의 숫자에 따라 대상들이 군집들에 할당되는 것임
- K-means 알고리즘을 이용
*군집분석 알고리즘
1. K-means 알고리즘
2. 가우시안 혼합모델
3. 커널 K-means 알고리즘
4. Spectral clustering
5. Latent Dirichlet Allocation
*K-means 알고리즘
- 일반적으로 사용되는 분할 클러스터링 알고리즘
- 알고리즘의 개념은 개체들과 그 개체가 속하는 클러스터의 중심과의 평균 유클리드 거리를 최소화하는 것임
- 클러스터의 중심은 그 클러스터에 속한 개체의 평균 혹은 중심(centroid) 이라 함
- 개체의 특성은 실수 값을 가지는 벡터로 표현함
- K-means에서 클러스터는 중력의 중심과 같은 무게 중심을 가지는 구형(sphere)으로 생각함
- 중심이 클러스터에 속한 개체들을 얼마나 잘 표현하였는가를 나타내는 척도(RSS)
- 각 클러스터에 속하는 모든 개체들에 대하여 각 개체와 중심까지의 제곱거리의 합으로 나타냄
- 초기 중심을 어떻게 선정하는가에 따라 성능이 크게 달라짐
- 기본적인 초기 중심은 무작위로 선정된 k개의 패턴 또는 패턴집합 범위 내의 임의의 k개의 좌표들로 구성됨
*K-means 클러스터링
1단계 : 최초의 k'평균'은 데이터 영역 내에서 무작위로 생성함
2단계 : 최초 클러스터링 단계로서 K클러스터는 최초의 k'평균'을 중심으로 각 개체는 k개의 중심 중 가장 가까운 곳으로 분류함
3단계 : 반복적인 클러스터링을 수행하는 단계로 개체를 바탕으로 k개의 중심을 다시 계산하고 분류를 반복함
4단계 : 종료 단계로 일정한 조건을 만족하여 k개의 중심이 더 이상 움직이지 않으면 종료함

*가우시안 혼합모델
- 패턴분석에 있어서 데이터의 특성을 분석하는 것이 매우 중요함
- 데이터의 분포 특성을 알기 위해 적절한 확률밀도함수를 가정하여 데이터 분포를 만드는 것이 확률분포모델임
- 주어진 표본 데이터의 집항의 분포밀도를 하나의 확률밀도함수로 모델링하는 방법을 개선하여 복수의 가우시안 확률밀도함수로 모델리하는 방법
- 복잡한 입력데이터를 각 가우시안 분포함수의 평균과 분산값으로 모델링함으로써 연산량을 줄일 수 있음
*커널 K-means 알고리즘
- K-means 알고리즘은 선형으로 분리 가능한 경우 완벽하게 클러스터로 분리되지만 비선형일 경우 커널 K-means 알고리즘을 사용
- K-means와 동일한 방식을 적용하지만, 차이점은 거리의 계산에서 유클리드 거리를 대신해서 커널을 사용함
*Spectral clustering
- 선형분리가 불가능한 데이터를 가능한 데이터로 변환하여 처리함
- 데이터 군집화를 그래프 분할 문제로 바꾼 것으로, 특정 목적함수를 최적화하려는 그래프 분할을 찾는 문제로 볼수 있음
- 주어진 데이터 포인트를 사이에 유사도를 나타내는 유사도 행렬 A를 구성하고 이 행렬의 고유벡터를 이용하여 원본데이터를 군집화하는 기법임
- 유사도 행렬을 구하는 과정과 그래프 분할의 과정으로 구분
- 유사도 행령이 블록대각 행렬을 이룰 때 최적의 결과를 보이는 것으로 알려짐
*Latent Dirichlet Allocation
- 정보검색에서 문서 모델링은 중요한 의미가 있음
- 문서 모델링이란 개별 문서 더 나아가 문서 컬렉션(corpus)을 표현하는 방법을 찾는 것임
- 이러한 문서분류 방법 중 가장 널리 사용하는 기법으로, 문서가 다양한 주제로 이루어졌다는 전제하에 주어진 문서에 대하여 각 문서에 어떤 주제들이 존재하는지에 대한 확률모형임
*범주형 자료분석
- 범주형 자료분석은 변수들이 이산형 변수일 때 주로 사용하는 분석임
- 명목적(nomial) 변수 : 성별, 종교, 지역
- 서열적(ordinal) 변수 : 사회계층, 태도
- 범주형 변수를 다룰 때는 일반적으로 그 빈도수를 세서 표를 작성(해당 표를 "분할표"라고함)
- 분할표를 기반으로 범주별 비교를 하고 범주형 변수의 독립성, 동질성 검정 등의 카이제곱 검정을 함
- 비율의 비교 : 상대위험도(relative risk), 오즈비(odds ratio)
*상대위험도(relative risk)
- 한 변수의 범주 별 다른 변수의 비율을 상대적으로 비교할 때 쓰이며 첫 범주에 속할 확률 추정량과 두 번째 범주에 속할 확률 추정량의 비로 정의됨
- 확률은 각 범주의 비율로 추정됨
*오즈비(odds ratio)
- 오즈비는 오즈(성공확률,실패확률)의 각 범주별 비율로 정의되며 상대위험도 보다 조금 더 유연한 특징을 보임
- 상대위험도는 매우 직관적인 척도지만 한 변수의 수를 고정시킨 조사에서는 사용이 불가능하다는 단점이 있음
오즈비는 이러한 경우에도 문제 없이 사용될 수 있으며 대칭적으로 구해지기 때문에 반응변수와 설명변수의 구별 없이 같은 값을 제시해 줌
- 분할표에서 자주 사용되는 것은 물론이고 확률을 선형화하는 여러 통계 모형에서 사용되므로 익숙해질 필요가 있음
- 상대위험도와 마찬가지로 두 변수가 연관이 없다면 오즈비는 1에 가까울 것이며 0에 가까워지거나 커질수록 밀접한 연관성을 보임
*카이제곱 독립성 검정
- 카이제곱 독립성 검정은 두 범주형 변수가 독립적으로 분포하는지를 테스트하는 검정임
- 분할표에서 진행되며 일반적으로 2x2가 아닌 여러 범주를 갖고 있는 경우에 사용함
- 카이제곱 독립성 검정의 기본적 아이디어는 관측빈도와 기대빈도의 차이를 비교하는 것임
- 기대빈도 : 두 변수가 독립일 떄의 빈도
- 카이제곱 통계량은 관측빈도와 기대빈도 차이의 변동을 정량화한 통계량임
- 기대빈도는 일반적으로 5를 기준으로함
- 카이제곱 통계량이 충분히 크다면 관측빈도와 기대빈도의 차이는 크다고 할 수 있음
- 만약 관측빈도와 기대빈도의 차이가 충분히 크면, 두 변수가 독립적이지 않다는 결론을 내리게 됨
*다변량분석(Multivariate Analysis)
- 다변량분석이란 연구자의 연구대상으로부터 측정된 두 개 이상의 변수들의 관계를 동시에 분석할 수 있는 통계적 기법을 말함
- 조사 중인 각 개인 혹은 각 대상물에 대한 다수의 측정치를 동시에 분석하는 방법이라 볼 수 있음
- 다수의 다변량 분석 기법은 일변량 분석과 이변량 분석의 확장 형태라 할 수 있음
*다변량분석 기법의 종류
1. 다중회귀분석
- 하나의 계량적 종속변수와 하나이상의 계량적 독립변수 간에 관련성이 있다고 가정되는 연구문제에 적합한 분석 기법임
- 다수의 독립변수의 변화에 따른 종속변수의 변화를 예측할 수 있음
- 회귀모형의 적합도를 분석할 수 있음
- 독립변수들이 종속변수를 설명하는 정도를 알 수 있음
- 종속변수에 대한 독립변수들의 상대적인 기여도를 파악할 수 있음
2. 다변량 분산분석과 다변량 공분산분석
- 다변량 분산분석은 두개 이상의 범주형 종속변수와 다수의 계량적 독립변수 간의 관련성을 동시에 알아볼 때 이용되는 통계적 방법임, 일변량 분산분석의 확장된 형태임
- 다변량 공분산분석은 실험에서 통제되지 않은 독립변수들의 종속변수들에 대한 효과를 제거하기 위해 다변량 분산분석과 함께 이용되는 방법임, 이변량 부분상관의 절차와 비슷함
3. 정준상관분석
- 하나의 계량적 종속변수와 다수의 계량적 독립변수 간의 관련성을 조사하는 다중회귀 분석을 논리적으로 확대시킨 것
- 다수의 계량적 종속변수와 다수의 계량적 독립변수 간의 상관관계를 알아보고자 할 때 쓰는 방법임
- 정준상관 분석의 기본원리는 종속변수군과 독립변수군의 두 변수군 간의 상관을 가장 크게 하는 각 변수군의 선형조합을 찾아내는 일임
- 종속변수군과 독립변수군 간의 상관을 최대화하는 각 변수군의 가중치의 집합을 찾아내는 것
4. 요인분석
- 많은 수의 변수들 간의 상호관련성을 분석하고 이들 변수들을 어떤 공통 요인들로 설명하고자 할 때 이용되는 기법임
- 많은 수의 원래 변수들을 이보다 적은 수의 요인으로 요약하기 위한 분석 기법을 말함
- 주로 검사나 측정도구의 개발과정에서 측정도구의 타당성을 파악하기 위한 방법으로 많이 사용되고 있음
- 탐색적 요인분석 : 연구자가 가설적인 요인을 설정하지 않고 얻어진 자료에 근거하여 경험적으로 요인의 구조를 파악함
- 확인적 요인분석 : 연구자가 사전에 요인의 구조를 가설적으로 설정하고 이를 검증함
5. 군집분석
- 각 표본을 표본들 간의 유사성에 기초해 한 집단에 분류시키고자 할 때 사용되는 기법임
- 집단에 관한 사전정보가 전혀 없는 각 표본에 대하여 그 분류체계를 찾을 경우 등
- 판별분석과 달리 군집분석에서는 집단이 사전에 정의되어 있지 않음
- 군집분석 단계
1단계 : 몇개의 집단이 존재하는가를 알아보기 위해 각 표본들 간의 유사성 혹은 연관성을 조사함
2단계 : 1단계에서 정의된 집단에 어떤 표본을 분류해 넣거나 혹은 그 소속을 예측함, 군집기법에 의해 나타난 그룹들에 대해 판별분석을 적용하게됨
6. 다중판별분석
- 종속변수가 비계량적 변수일 경우 다중판별분석이 이용됨
- 종속변수가 '남자/여자'와 같이 두 개의 범주로 나누어져 있거나, 혹은 '상/중/하'와 같이 두개 이상의 범주로 나누어져 있을 경우를 말함
- 다중회귀분석과 같이 독립변수는 계량적 변수로 이루어짐
- 판별분석은 각 표본이 여러 개의 범주를 가진 종속변수에 기초한 여러 개의 집단으로 분류될 때 적합함
- 다중판별분석의 주 목적은 집단 간의 차이를 판별하며, 어떤 사례가 여러 개의 계량적 독립변수에 기초하여 특정 집단에 속할 가능성을 예측하는 데 있음
7. 다차원 척도법
- 다차원 척도법은 두 표본의 유사성을 다차원 공간상의 거리로 나타낼 때 사용됨
8. 구조방정식모형
9. 컨조인트분석
*시계열분석
- 시계열(time series)자료 : 시간에 따라 관측되는 자료
- 수집된 시계열자료를 분석하여 미래를 예측(forecast) 하는 것임
- 시계열에서 나타나는 변동 : 우연변동, 계통변동
*평활법
- 미래에 대해 예측할 떄, 과거의 모든 자료를 동일하게 취급하여 계산한 예측값보다는 최근의 자료를 더 비중있게 취급하는 예측법이 더 합리적일 것임
- 이동평균볍 : 최근 일정 시점 자료들의 평균값을 이용하여 예측을 하는데, 일정 시점의 크기에 따라 그 결과가 달라짐
- 지수평활법 : 현시점에서 과거로 갈수록 가중치를 작게 주는 방법을 말함, 최근 자료에 더 큰 가중치를 주고 과거로 갈수록 가중치를 줄이는 것은 직관적으로도 타당하며, 계산법이 쉽고 많은 자료를 저장할 필요가 없다는 점에서 유용하게 사용되고 있음
*지수평활법
1. 단순지수평활법
2. 이중지수평활법
3. 계절지수평활법
*베이지안 확률론(Bayesian Probability)
- 지식의 상태를 측정하는 것이라고 해석하는 확률론임
- 18세기 통계학자 토마스 베이즈의 이름을 땀
- 현대적 기계학습 방법은 객관적 베이지안 원리에 따라 만들어짐
- 여러개념 중 가장 인기 있는 것 중 하나로 심리학, 사회학, 경제학 이론에 많이 응용됨
- 베이즈 정리는 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법임
- 사전확률과 사후확률 간의 관계에 대해 설명하는 정리를 말함
*베이지안 확률의 두 가지 시점
1. 객관적 관점에서 베이지안 통계의 법칙은 이성적, 보편적으로 증명될 수 있으며 논리의 확장으로 설명될 수 있음
2. 주관주의 확률 이론의 관점으로 보면 지식의 상태는 개인적인 믿의 정도로 측정할 수 있다는 것임
*딥러닝 분석
- 심층학습 또는 딥러닝은 여러 비선형 변환 기법의 조합을 통해 높은 수준의 추상화를 시도하는 기계 학습 알고리즘의 집합으로 정의되며, 큰 틀에서 사람의 사고방식을 컴퓨터에게 가르치는 기계학습의 한 분야라고 이야기할 수 있음
- 추상화 : 다량의 데이터나 복잡한 자료들 속에서 핵심적인 내용 또는 기능을 요약하는 작업
- 어떠한 데이터가 있을 때 이를 컴퓨터가 알아들을 수 있는 형태로 표현하고 이를 학습에 적용하기 위해 많은 연구가 진행되고 있음
- 컴퓨터비전, 음성인식, 자연어처리, 음성/신호처리
- 딥러닝(deep learning)은 머신러닝의 3가지 패러다임 중에서 신경모형 패러다임에 속함
- 연결주의론의 최신 버전이라고 할수 있음
- 딥러닝의 딥(deep)이라는 말은 신경망의 층(layer)이 깊고 각 층마다 고려되는 변수가 많다는 의미임
- 천층망 : Shallow Network, 2~3개의 층으로 되어 있는 신경망
- 심층망 : Deep Network, 2~3개 이상의 층으로 구성되어 있는 신경망
- 딥러닝에서 깊이를 나타내는 층의 개수는 입력층과 출력층 사이에 있는 은닉층(hidden layer) 개수에 하나를 더하면됨
- 이러한 이유로 딥러닝을 심층신경망(DNN)이라고 함
*컨볼루션 신경망(CNN, Convolution Neural Network) : 영상, 이미지와 같은 데이터를 처리
- 이미지 인식 분야에 큰발전을 가져옴
- 컴퓨터비전 분야에서 특화된 방법으로 사용
- 역전파 기반의 인공신경망의 한 종류
- 3차원 데이터의 공간적 정보를 유지한 채 원하는 특성을 추출하는 데 탁월함
- 컨볼루션 신경망은 인공신경망 알고리즘의 앞 부분에 컨볼루션 기법을 추가한 알고리즘임
- 입력한 데이터를 컨볼루션으로 특징 추출 등의 전처리 후, 추출된 특징을 기반으로 신경망을 이용하여 분류해 내는 것을 말함
- 페이스북의 딥페이스 얼굴인식
*순환 신경망(RNN, Recurrent Neural Network) : 음성인식 및 음악, 시퀀스가 있는 문자열 데이터를 처리
- 순환신경망은 음성이나 언어 등 연속적으로 되풀이되는 입력 데이터를 사용하는 모델로서, 아래와 같은 다양한 분야에서 사용되고 있음-> 음성인식, 자연어처리
- RNN에 대한 기본적인 아이디어는 순차적인 정보를 처리한다는 데 있음
- 일반적인 신경망은 각각의 입출력이 서로 독립적이라고 가정하지만, RNN은 순서가 있는 정보를 입력 데이터로 사용함
- 음악, 문자열, 동영상 등에 사용
- 일반적인 인공신경망은 각 층의 뉴런이 연결되어, 데이터를 입력하면 입력층에서 시작해 은닉층을 거쳐 출력층까지 전방으로 진행이됨
- RNN은 일반 신경망과 달리 은닉층의 결과가 다시 같은 은닉층의 입력으로 돌아오는 입력을 만듦
- 마치 메모리와 같은 역할을 하여 데이터의 순차적인 변화를 고려한 모델을 만들 수 있게 해줌
- RNN의 구조에서는 은닉츠의 뉴런이 다시 같은 뉴런으로 돌아오는 화살표를 볼 수 있음
- 기존의 일반 신경망에서 추가된 구조로, 순화가중치라고 함
*심층 신뢰망(DBN, Deep Belief Network)
- 심층 신뢰망은 입력층과 은닉층으로 구성되어 있는 RBM을 층층이 쌓아 올린 형태로 연결한 신경망임
- RBM을 여러 층으로 쌓아 올려 연결하기 때문에 심층신뢰망이라고함
- RBM : 제한된 볼츠만 머신
- 사전 학습(pre-training)을 하여 깊은 신경망 구조에서 나타나는 경사감소소멸 현상을 해결함
- RBM의 목적은 심층망 구조에서 일반적으로 나타나는 에러의 정보 손실을 최소화하는 것임
- 입력층에서 입력된 데이터의 특성을 일종의 비지도학습 형태로 반복 학습하여 은닉층으로 전달하며 에러율을 최소하하는 것을 말함
- 이를 위해 RBM은 에너지-기반모델(EBM)을 사용함
- 역전파 기법이 적용되며 최종 가중치를 계산하는 것이 심층신뢰망의 목표임
*비정형 데이터 마이닝 과정
- 탐색 => 이해 => 분석
- 탐색 : 질의, 집합연산, 재귀 및 팽창 등의 작업을 수행함
- 이해 : 통게, 분배, 특징 선택, 군집화, 분류 편집, 시각화 등의 작업을 수행함
- 분석 : 경향, 상관관계, 분류 등의 작업을 수행함
*비정형 데이터마이닝 기법
1. 텍스트 마이닝
2. 웹 마이닝
3. 오피니언 마이닝
4. 소셜 네트워크 분석
*앙상블(Ensemble) 기법
- 주어진 데이터를 이용하여 여러 개의 서로 다른 예측 모형을 생성한 후, 이러한 예측 모형의 예측 결과를 종합하여 하나의 최종 예측결과를 도츨해 냄
- 목표변수의 형태에 따라 분류분석 및 회귀분석에도 사용이 가능함
- 분류분석에 사용하면 '분류앙상블'
- 회귀분석에 사용하면 '회귀앙상블'
- 과소적합(Underfitting)과 과대적합(Overfitting)을 예방함
- 앙상블 모형 : 배깅(Bagging), 부스팅(Boosting), 랜덤 포레스트(Random forest)
*모수통계 : 모집단의 특성에 대한 정보(분포의 형태와 모수에 대한 사전정보)가 충분하고 변수의 척도가 등간척도 이상으로 측정된 경우 적용될 수 있는 통계분석 방법
*비모수통계 : 모집단의 분포형태나 모수에 대한 정보가 부족해 모집단의 특성에 대한 가정을 세우기 어렵거나 자료의 척도가 명목척도나 서열척도인 경우 적용되는 통계분석 방법
*비모수 통계기법의 종류




*비모수 통계기법 적용 조건
- 자료가 나타내는 모집단의 현상이 정규분포가 아닐 때
- 자료가 나타내는 모집단의 현상이 정규분포로 적절히 변환되지 못할 떄
- 자료의 표본(sample) 수가 적을 떄
- 자료들이 서로 독립적일 때
- 변인의 척도가 명목척도나 서열척도 일 때
- 분석에 이용되는 자료가 어떤 범주별로 어떤 사건이 발생한 수를 반영하는 계산자료인 경우
- 모집단 분포의 모수에 대해서 통계적 추론을 하지 않는 경우
- 분석에 이용되는 통계량의 확률분포가 모집단의 확률분포의 구체적인 사항에 의하여 영향을 받지 않고, 오직 모집단의 분포의 대칭성이나 연속성과 일반적인 가정에 근거를 둔 경우에 적절하게 변화되지 못하는 경우
- 주로 서열척도나 명명척도일 경우
'빅데이터분석기사' 카테고리의 다른 글
| 빅데이터 분석 기사 필기 요약 4과목 (0) | 2021.06.14 |
|---|---|
| 빅데이터 분석 기사 필기 요약 3과목 (0) | 2021.06.14 |
| 빅데이터 분석 기사 필기 요약 2과목 (0) | 2021.06.14 |
| 빅데이터 분석 기사 필기 요약 1과목 (0) | 2021.06.14 |
| 빅데이터 분석 기사(필기) (0) | 2021.02.01 |
